Peter King's composition of 23-spliced treble bob major was recently rung on handbells for the first time, having been rung only twice (I think) on tower bells. The band was Jonathan Agg, Lucy Warren, Julian Howes and Alan Reading. Posting in the Bellringers Facebook group, Philip Earis wrote: 

The ASCY handbell peal of 23 spliced Treble Bob major rung at the weekend is, in terms of complexity, one of the most impressive ringing achievements of all time. It's an order of magnitude more challenging than any other peal of 23 spliced major that's been rung. "Oh, to be alive in such an age!"

There followed some discussion about what makes the composition so difficult, and I think it's worth looking into here. The first thing to explain is the significance of the treble bob classification. Methods in which the treble's path is treble bob hunting are classified as either treble bob, delight or surprise. The reasons for this subdivision are lost in the mists of time, but the classification itself is based on a simple rule.

The key is what happens when the treble moves between dodging positions: hunting up from 2nd place to 3rd place, up from 4th place to 5th place, up from 6th place to 7th place, and similarly hunting down in the second half of the lead. These points in the lead are called cross sections (a section is the block of four rows while the treble is in one dodging position).

In a surprise method, every cross section has an internal place made, meaning a place other than leading or lying behind. In a treble bob method, none of the cross sections have internal places: the place notation is always 18 (for major) when the treble hunts to a new dodging position. In a delight method, some cross sections have internal places and some don't.

Over time, surprise methods have come to be seen as more desirable. On 8 or more bells, the vast majority of treble dodging methods that have been rung and named are surprise methods. In Change-Ringing on Handbells Volume 2 there is an attempt at an explanation for this preference:

In the evolution of the standard repertoire, surprise methods became preferred over delight or treble bob methods, especially on eight or more bells. This is because internal places cause deviation from plain hunting, through the places themselves and through the dodging that they cause, so methods with more internal places tend to have more dodging, more place-work, and more differences from plain hunting or treble bob hunting. This makes them more difficult and therefore more satisfying and prestigious when mastered.

That analysis is most convincing for right-place methods - these are methods in which the place notation when moving to a handstroke row is always X. In this case internal places cause dodging, either within the sections or at the cross-sections. There always have to be some internal places within the sections, when the treble dodges, otherwise all the bells would be dodging simultaneously and the rows would repeat. So it's the cross-sections that give scope for a method to have more or fewer internal places - hence using the number of internal places at cross-sections as the basis for a classification which in turn gives a rough guide to the difficulty of the method.

The text goes on to explain that there are plenty of interesting and difficult delight methods, and mentions Peter King's composition as containing treble bob methods that were deliberately designed to be as difficult as possible.

I would now like to look at the structure of treble bob methods a little more closely, because I think the above analysis is an over-simplification. Let's start with right-place methods and consider the consequences of the conditions defining a treble bob method.

The main point is that in general there can't be an internal place (handstroke then backstroke, as we are discussing right-place methods) followed by another internal place at the next handstroke/change. This is because one of the internal places would have to be at a cross section. Yorkshire places are impossible. Even a double dodge is impossible. Here is Barlow Treble Bob Major, which has typical features: single dodges, blocks of plain hunting or treble bob hunting, turnaround places.

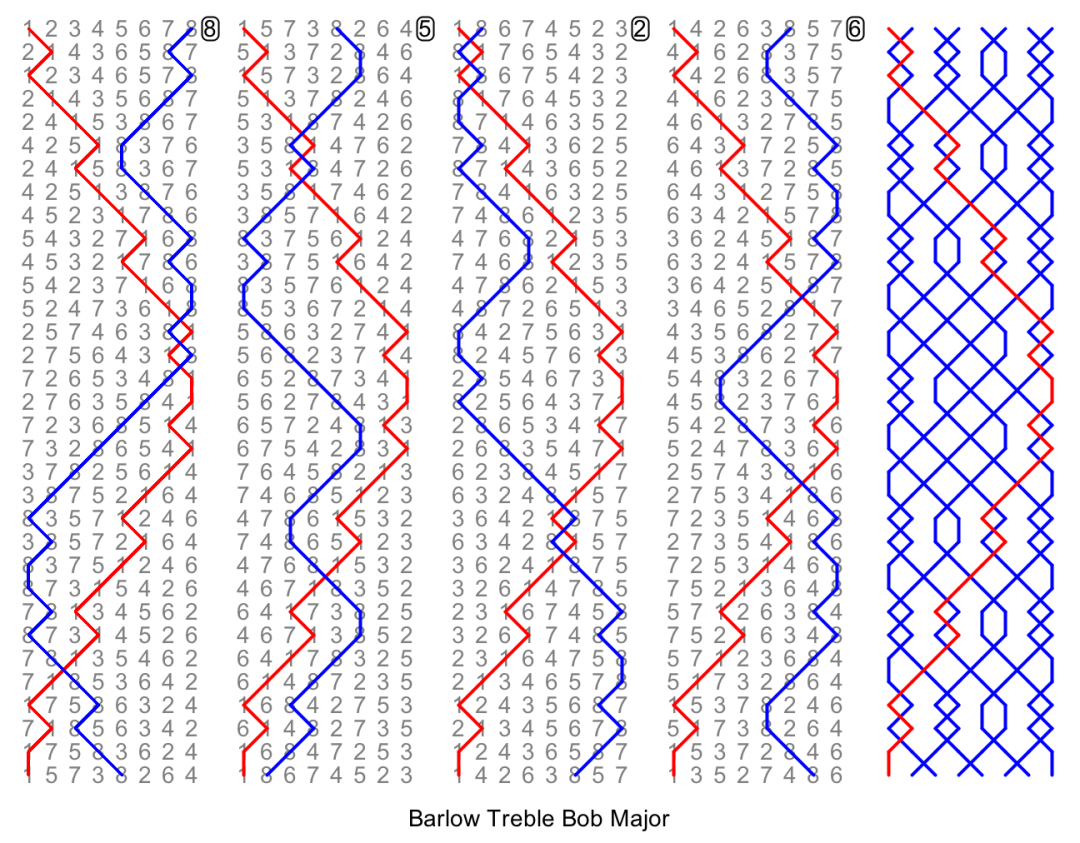
The half lead and lead end are not considered to be cross sections, so it is possible to have place notations other than 18 at those positions. Barlow demonstrates this with 58 at the half lead. This opens up the possibility of slightly longer pieces of work around the half lead or lead end. An example is Kalamazoo, which also has a longer backwork obtained by making 7th place at a position other than the half lead - usually this is considered undesirable in surprise methods.

An example with a 2nd place lead end and consequent place-work around the lead end as well as around the half lead is Newbury.

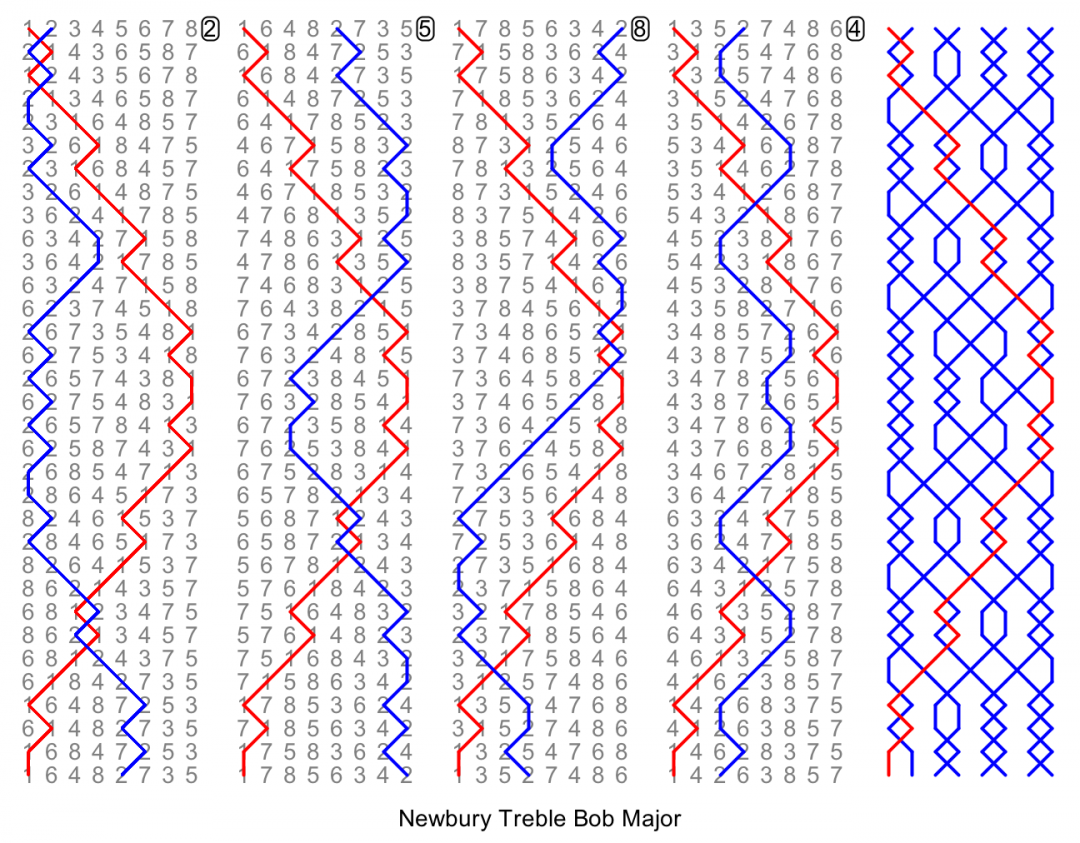
These examples are typical of what's possible. I'm not sure it's true to say that the methods are easier than surprise methods. In fact, ringing several of them in a peal of spliced might be more difficult, because they lack the distinctive longer structures that we use as learning aids in the standard methods. However, the variety and richness of different pieces of work, seen in surprise methods, is not available. Only 15 right-place treble bob major methods have been named, and three of them are little methods (treble not going all the way to the back), leaving just 12 full-length methods.

Now, back to Peter King's composition of 23-spliced. All the methods are wrong-place, which means that a bit more variety of work is possible, but long pieces of work are rare. Most of the methods were designed for the composition and given thematic names: Awful, Bizarre, Crazy, Diabolical etc (and the alphabetical sequence continues). The exceptions are Blue Nile and Easton Neston, previously named and also difficult. The lines of Awful and Unpleasant give a good impression of the whole peal:

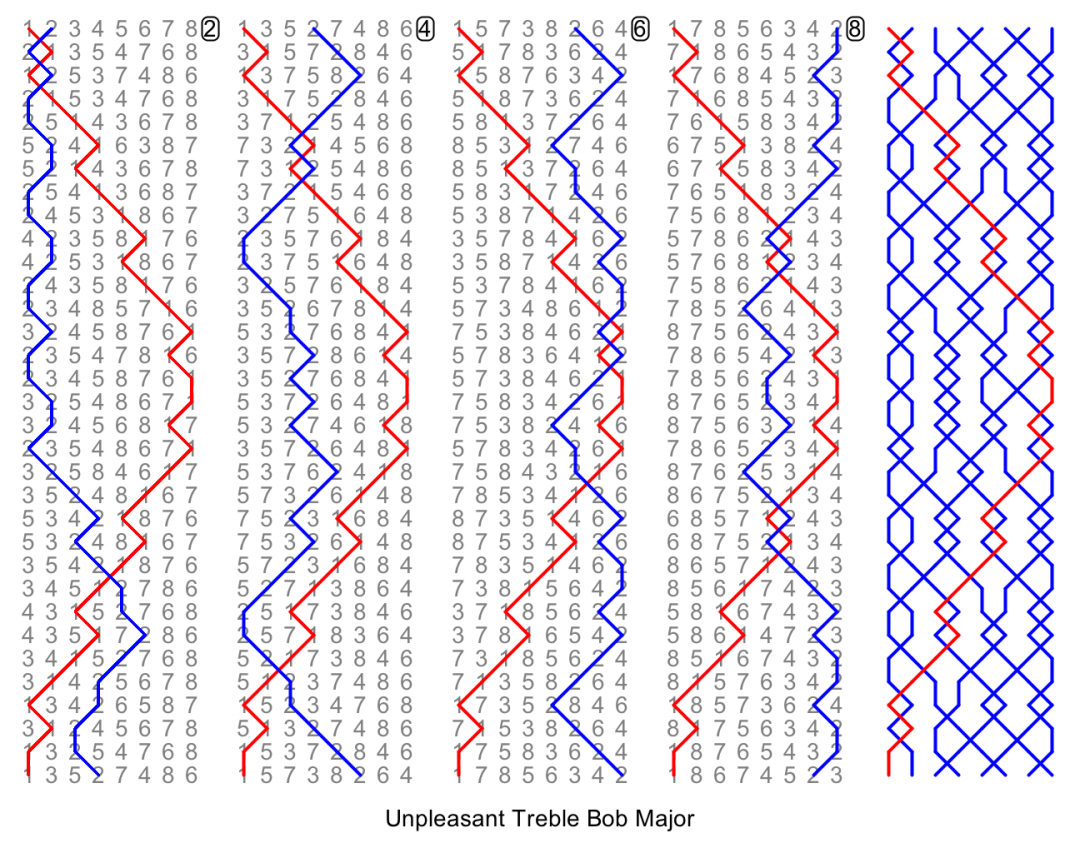
Notice the unusual sequence of places at the end of 2nd place bell in Awful, and the repetition of point 5ths, 6ths, treble bob in 6th place bell Unpleasant. Any of these methods would be a challenge to ring individually, and learning 23 of them for a peal of spliced would be really really difficult.

Hats off to the band who did it!