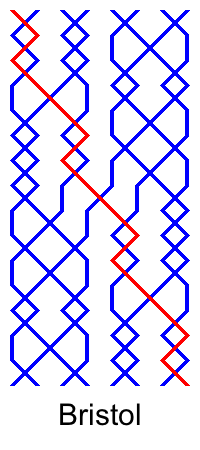
Double methods are those in which the frontwork is the backwork upside down. This means that the line of the method has rotational symmetry: it looks the same if rotated by 180 degrees about the point at which it passes the treble in the central position of the change (4-5 in Major). It also means that the grid of half a lead has rotational symmetry, which we can see by looking at Bristol.

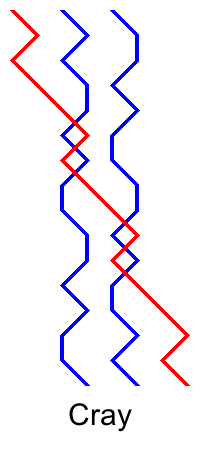
Something I realised only recently is that on handbells, you can simultaneously ring half a lead of one place bell and its rotationally symmetric partner. Below are some examples from 23-spliced. Note that although Cray isn't a double method, its half lead grid is rotationally symmetric, and it can be converted into a double method by ringing it with 8ths place at the lead end (giving Norfolk) or 7ths place at the half lead (giving Derwent). The examples are for the first half of the lead, but it is also possible to ring a rotationally symmetric pair in the second half of the lead.  

The trebles can also ring a rotationally symmetric half lead, when the 2nd is the place bell that passes the treble in 4-5, for example 5ths place bell in Bristol.

Furthermore, each handbell position (1-2, 3-4, 5-6, 7-8) has its own rotationally symmetric half lead, and in the plain course, they are all rung simultaneously.

When thinking about symmetry in pairs of place bells, we are more accustomed to noticing when we are ringing two place bells that are the reverse of each other, meaning that the pair crosses at the half lead and then repeats the work backwards. These are generally easy leads to ring, because it's possible to ring the second half by reversing the work of the first half, and crossing at the half lead is a good landmark. Ringing a rotationally symmetric half lead doesn't seem to be so helpful, and in fact some of those leads are the ones that we have found most difficult. I have always found that ringing 4th and 5th place bells in Superlative, or the second half of 2nd and 7th place bells, requires care. In Double Dublin, 2nd and 8th place bells seem very difficult because of the overlap between the fishtail and the whaletail. In Cray, 3rd and 5th place bells have a similar character to 4th and 5th place bells in Superlative, but 2nd and 7th place bells are less of problem because it's only necessary to know that the long dodges overlap by 3, or to start and stop dodging according to the position of the treble.

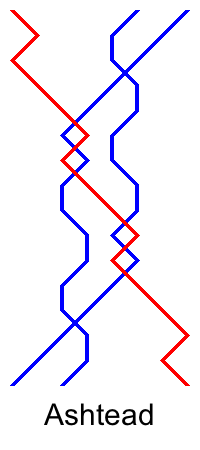
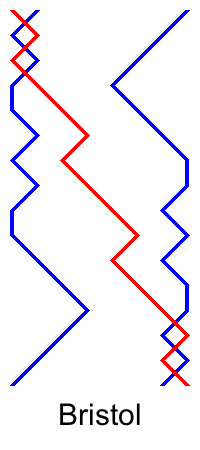
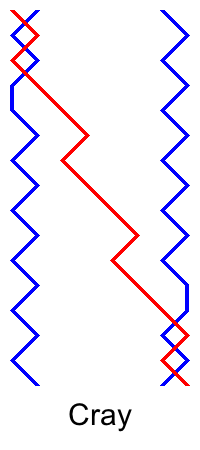
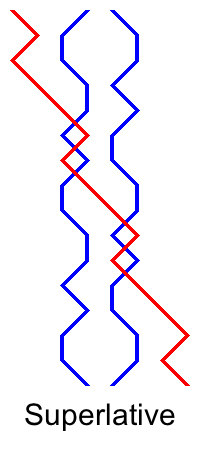
When I wrote about symmetry before, I gave a composition for a quarter of Spliced Surprise Major in which 7-8 always ring symmetrical leads, and another composition in which 5-6 and 7-8 always ring symmetrical leads. The obvious question now is whether we can get a composition of spliced double methods in which 5-6 and 7-8 always ring rotationally symmetrical half leads.

The answer is: almost. It turns out that it's not possible for 7th and 8th place bells to be a rotationally symmetric pair in the first half lead, because that would require 5-6, 3-4 and 1-2 to also be ringing their rotationally symmetric leads. That would require the 2nd to pass the treble in 4-5 in the first half of the lead, which is impossible because it starts by going below the treble.

The composition I have come up with starts with a whole lead of an M group method, in which 5-6 and 7-8 ring their ordinary symmetrical leads. It then continues with 6 other methods, all with different place bell orders, rung half a lead at a time. Each method is rung once in the first half of a lead and once in the second half of a lead. Every half lead has 7ths place made, and every lead end is 8ths place. Strictly speaking this means that the first and second half leads with a particular grid are two different methods, one with 2nds/7ths at the lead end and half lead, and one with 8ths in both places. A further complication is that one of the methods is group A, so its 8ths place lead end version doesn't exist because it would come round after one lead. Anyway, we can consider that the composition contains 6 rotationally symmetric grids, which are rung with the appropriate half lead and lead end places. Unfortunately the M group method can't be a double method, because the half lead would be repeated later.

1344 Spliced Surprise Major (7m)
Simon J Gay

                12345678
------------------------
Hampshire       24356871
Hampshire       14263857
Ashtead         68472531
Maypole         16482735
Lancashire      46283751
Peterborough    18674523
Cambridge Blue  24365871
Superlative -   17856423
Superlative     43527681
Cambridge Blue  15748362
Peterborough    54738261
Lancashire      14537286
Maypole         75846321
Ashtead         13425678
------------------------
Half lead place is always 78, except in Hampshire.
Lead end place is always 18.
- = 16
6 part, calling 1678 instead of - in parts 3 and 6.

5-6 and 7-8 always ring rotationally symmetric half leads,
except in Hampshire where they ring a symmetrical lead.