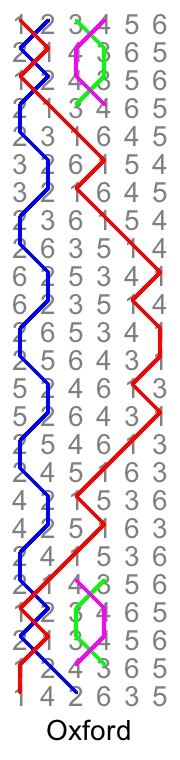
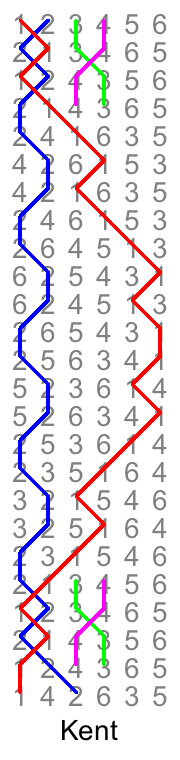
In the campaign of trying to understand the structure of methods by thinking of them as compositions, let's move on to treble bob. Now the base method is treble bob hunting instead of plain hunting, and again we will consider variations with respect to pure treble bob hunting as if they are bobs that affect the coursing order. Unlike plain hunting, treble bob hunting is false, so the aim is to introduce enough variations to give a true composition, as well as producing a coursing order that corresponds to a plain bob lead end.

First consider Kent. As usual the coursing order is 124653. The composition for a lead of Kent its that the 2nd swaps with each other bell in turn, giving the sequence of coursing orders 142653, 146253, 146523, 146532. This is a cyclic rotation of the non-treble bells, so it produces a plain bob lead end, 142635.

This composition is still false, because at the beginning (and end) of the lead, all the bells dodge. To fix that, the 3rd and 4th make Kent places, changing the coursing order to 123654 and back to 124653 (the first time) and then to 136542 and back to 146532 (the second time).

When ringing (or especially conducting) Kent, we know that the treble takes the place of the slow bell in the coursing order of the other bells. We can see how this works by writing each coursing order with the 2nd at the front: 246531, 265314, 253146, 231465, 214653. Looking at the bells other than the 2nd in each case, replacing 1 by 2 would indeed give rotations of 24653. 

Oxford is the same except that it has a different way of removing the falseness at the beginning and end of the lead. The 3rd and 4th swap at the beginning of the lead, giving coursing order 123654. Then the 2nd swaps with each bell in turn, giving the sequence 132654, 136254, 136524, 136542. Finally the 3rd and 4th swap back to give 146532.